 ®
®
Postfix Notation
Mini-Lecture
Every student of computer science should understand the concept of postfix notation and the use of stacks. For students of computer architecture this postfix notation mini-lecture is really an aside to show you how mind-bogglingly useful the concept of a stack is. It doesn't make any difference whether the stack is implemented in hardware and supported by the microarchitecture or simulated using an array and totally a creation of the high-level language programmer.
At some point in your career you will be asked to write a
program that can interpret an expression in a notation similar to
that of algebra. Getting something like (A+B)/(C-D)
right can seem like a daunting task, especially when you are asked
to write code that will interpret any valid expression. It
turns out to be surprisingly easy if the problem is decomposed into
two steps: translation to postfix notation and evaluation of the
postfix notation expression. This is not a new idea... it was described by Donald Knuth in 1962 and he was writing a history! The stack algorithm illustrated below was described by Edsgar W. Dijkstra in 1961.
Postfix Notation
Postfix notation is a way of writing algebraic expressions
without the use of parentheses or rules of operator precedence. The
expression above would be written as AB+CD-/ in
postfix notation. (Don't panic! We'll explain this in a moment.)
Postfix notation had its beginnings in the work of Jan Łukasiewicz ![]() (1878-1956), a
Polish logician, mathematician, and philosopher. Łukasiewicz
developed a parenthesis-free prefix notation that came to be called
Polish notation and a postfix notation now called Reverse Polish Notation or RPN. From these ideas, Charles Hamblin developed a postfix notation for use in computers. Łukasiewicz's work dates from about 1920. Hamblin's work on postfix notation was in the mid-1950's. Calculators, notably those from Hewlett-Packard, used various postfix formats beginning in the 1960s.
(1878-1956), a
Polish logician, mathematician, and philosopher. Łukasiewicz
developed a parenthesis-free prefix notation that came to be called
Polish notation and a postfix notation now called Reverse Polish Notation or RPN. From these ideas, Charles Hamblin developed a postfix notation for use in computers. Łukasiewicz's work dates from about 1920. Hamblin's work on postfix notation was in the mid-1950's. Calculators, notably those from Hewlett-Packard, used various postfix formats beginning in the 1960s.
In this mini-lecture we will use variables represented by single
letters and operators represented by single characters. Things are
more complicated in real life. Variables have names composed of
many characters and some operators, like ** for
exponentiation, require more than a single character. However, we
can make these simplifications without loss of generality.
In our simplified examples, each variable is represented by a single letter and each operator by a single character. These are called tokens. In a more complex implementation, your program would still scan a series of tokens, but they would likely be pointers into symbol tables, constant pools, and procedure calls for operators.
Evaluating Postfix Notation
Evaluating an expression in postfix notation is trivially easy if you use a stack. The postfix expression to be evaluated is scanned from left to right. Variables or constants are pushed onto the stack. When an operator is encountered, the indicated action is performed using the top elements of the stack, and the result replaces the operands on the stack.
Let's do an example using the postfix expression
AB+CD-/. In order to see what's going on as the
expression is evaluated, we will substitute numbers for the
variables. The expression to be evaluated becomes 9 7 + 5 3 -
/. This is equivalent to (9 + 7) / (5 - 3) so
we expect the answer to be eight. Click the "Go" button at the
right to see an animation showing the evaluation of the
expression.
You will see the expression scanned from left to right. A yellow highlight shows the term currently being scanned. The digits in the expression are pushed onto the stack and the operators are performed.
Experiment with the animation until you are sure you understand what's going on.
Now that you see how easy it is to evaluate an expression that's
in RPN form, you will want to convert ordinary infix expressions to
RPN so that you can evaluate them. That turns out to be easy, too,
if you use a stack.
Converting Infix to Postfix
 |
||||||||||||||||||||||||
 |
||||||||||||||||||||||||
We know that the infix expression (A+B)/(C-D) is
equivalent to the postfix expression AB+CD-/. Let's
convert the former to the latter.
We have to know the rules of operator precedence in order to convert infix to postfix. The operations + and - have the same precedence. Multiplication and division, which we will represent as * and / also have equal precedence, but both have higher precedence than + and -. These are the same rules you learned in high school.
We place a "terminating symbol" ![]() after the infix expression to serve
as a marker that we have reached the end of the expression. We also
push this symbol onto the stack.
after the infix expression to serve
as a marker that we have reached the end of the expression. We also
push this symbol onto the stack.
After that, the expression is processed according to the following rules:
- Variables (in this case letters) are copied to the output
- Left parentheses are always pushed onto the stack
- When a right parenthesis is encountered, the symbol at the top of the stack is popped off the stack and copied to the output. Repeat until the symbol at the top of the stack is a left parenthesis. When that occurs, both parentheses are discarded.
- Otherwise, if the symbol being scanned has a higher precedence than the symbol at the top of the stack, the symbol being scanned is pushed onto the stack and the scan pointer is advanced.
- If the precedence of the symbol being scanned is lower than or equal to the precedence of the symbol at the top of the stack, one element of the stack is popped to the output; the scan pointer is not advanced. Instead, the symbol being scanned will be compared with the new top element on the stack.
- When the terminating symbol is reached on the input scan, the stack is popped to the output until the terminating symbol is also reached on the stack. Then the algorithm terminates.
- If the top of the stack is a left parenthesis and the terminating symbol is scanned, or a right parenthesis is scanned when the terminating symbol is at the top of the stack, the parentheses of the original expression were unbalanced and an unrecoverable error has occurred.
Click the "go" button on the animation to see how
(A+B)/(C-D) is transformed to the postfix expression
AB+CD-/. You can use "reset" and "go" to run the
animation several times.
When an infix expression has been converted to postfix, the variables are in the same order. However, the operators have been reordered so that they are executed in order of precedence.
Understanding Table 5-21 in Tanenbaum
The rules expressed as a list in the previous section are shown in a nice, unambiguous table in Structured Computer Organization by Andrew Tanenbaum and Todd Austin (2013). Unfortunately, for some students the "train" analogy used by Tanenbaum and Austin gets in the way of seeing how to use this table. Here is the material from Tanenbaum and Austin presented in terms of a stack rather than with the train analogy. The "scan pointer" is a way of keeping track of which token in the input expression is being examined. It is analogous to the yellow highlight in the animation.
- The terminating symbol
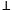 is appended to the expression to be
converted and also pushed onto the stack.
is appended to the expression to be
converted and also pushed onto the stack. - The scan pointer is set to the leftmost symbol of the input expression. Scanning proceeds left-to-right.
- If a variable is encountered, it is copied to the output and the scan pointer is advanced.
- If an operator symbol is encountered, it is compared with the symbol at
the stop of the stack using Table 5-21, and one of the following
actions is taken depending on the number from the table:
- The symbol being scanned is pushed onto the stack and the scan pointer is advanced.
- The stack is popped and the symbol from the stack is copied to the output. The scan pointer is not advanced.
- The symbol at the top of the stack is deleted and the scan pointer is advanced. (This is how parentheses are removed from the infix expression.)
- Done. The expression has been converted and the algorithm terminates successfully.
- Error. The parentheses in the original expression were not balanced, and the expression cannot be converted.
- After each action is taken, a new comparison is made between the symbol being scanned, which may be the same as in the previous comparison, and the symbol at the top of the stack. This continues until the algorithm terminates.
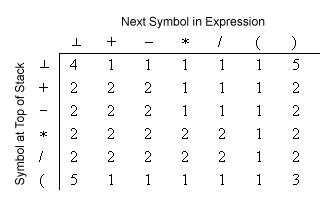 |
| Figure 5-21 from Tanenbaum and Austin (2013). Find the symbol at the top of the stack on the left and the symbol being scanned across the top. The action to take is indicated by the number at the intersection of the row and column. |
Cite this paper as:
Please take a moment to If you found this helpful, please click the +1 button at the top right.
References
Dijkstra, Edsgar W. (1961), "Algol 60 translation: An algol 60 translator for the x1 and making a translator for algol 60," Mathematisch Centrum Report MR 34/61.
Knuth, Donald E. (1962), "A History of Writing Compilers," Computers and Automation, December, 1962, reprinted in Pollock, Barry W., ed. Compiler Techniques, Auerbach Publishers, 1972.
Tanenbaum, Andrew S. and Todd Austin (2013), Structured Computer Organization, Prentice-Hall. (Earlier editions contain the same discussion.)
Further Reading
You can find a short biographical article about Łukasiewicz in the Wikipedia and another biographical article at the University of St. Andrews. These links will open new windows.
Back to the Web Lectures Table of Contents
Copyright © by Bob Brown. Some rights reserved.
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License.
Last updated:
2016-05-06 13:15
Originally published:
April, 2001